Diferenças entre edições de "Regressão linear"

Edição atual desde as 12h27min de 13 de outubro de 2008

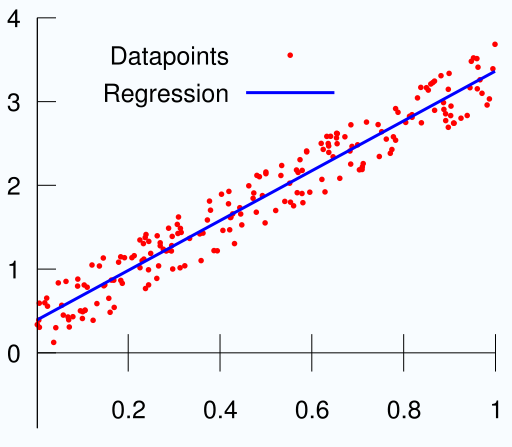Em estatística, regressão linear é um método para se estimar a condicional (valor esperado) de uma variável y, dados os valores de algumas outras variáveis x.

A regressão, em geral, trata da questão de se estimar um valor condicional esperado.

A regressão linear é chamada "linear" porque se considera que a relação da resposta às variáveis é uma função linear de alguns parâmetros. Os modelos de regressão que não são uma função linear dos parâmetros se chamam modelos de regressão não-linear.

Índice

1 Equação da Regressão Linear
- 1.1 Cálculo dos factores e
  - 1.1.1 Desenvolvimento
  - 1.1.2 Memorização
- 1.2 Intervalos de confiança
2 Bibliografia

Equação da Regressão Linear

Para se estimar o valor esperado, usa-se de uma equação, que determina a relação entre ambas as variáveis.

$Y_i = \alpha + \beta \, X_i + \epsilon_i$

Em que:

$Y_i$ - Variável explicada (dependente); é o valor que se quer atingir;

$\alpha$ - É uma constante, que representa a intercepção da recta com o eixo vertical;

$\beta$ - É outra constante, que representa o declive da recta;

$X_i$ - Variável explicativa (independente), representa o factor explicativo na equação;

$\epsilon_i$ - Variável que inclui todos os factores residuais mais os possíveis erros de medição. O seu comportamento é aleatório, devido à natureza dos factores que encerra. Para que essa fórmula possa ser aplicada, os erros devem satisfazer determinadas hipóteses, que são: serem variáveis normais, com a mesma variância $\sigma^2\,$ (desconhecida), independentes e independentes da variável explicativa X.

Cálculo dos factores $\alpha$ e $\beta$

$\hat{\alpha}=\frac{\sum \,X^2 \sum Y -\sum \,(X Y) \, \sum X}{n \, \sum_\,X^2-(\sum X)^2}$

$\hat{\beta}=\frac{n \sum \,(X Y)-\sum X \, \sum Y}{n \, \sum_\,X^2-(\sum X)^2}$

Definindo $\overline{X} = \frac {\sum X} {n}$ e $\overline{Y} = \frac {\sum Y} {n}$ , temos que $\hat{\alpha}$ e $\hat{\beta}$ se relacionam por:

$\hat{\alpha}=\overline{Y}-\hat{\beta} \, \overline{X}$

Desenvolvimento

O objectivo é determinar $\alpha$ e $\beta$ de forma que a soma dos quadrados dos erros seja mínima, ou seja, devemos minimizar

$\sum (Y_i \, - \, \beta \, X_i \, - \, \alpha)^2$

Desenvolvendo este quadrado e eliminando os termos constantes (ou seja, aqueles que não têm termos em $\alpha$ e $\beta$ , chega-se a:

$\beta^2 \, \sum X^2 \, + \, n \, \alpha^2 \, - \, 2 \, \beta \sum (X Y) \, - \, 2 \, \alpha \, \sum Y \, + \, 2 \, \alpha \, \beta \, \sum X$

A partir desse ponto, pode-se resolver usando-se cálculo (tomando as derivadas parciais, etc), ou através de uma transformação de coordenadas:

$\alpha \, = \, \alpha_1 \, - \, \frac { \sum X } { n } \, \beta$

ou

$\alpha \, = \, \alpha_1 \, - \, \beta \, \overline{X}$

Transformando a expressão a ser minimizada em:

$\beta^2 \, \sum X^2 \, + \, n \, \alpha_1^2 \, - \, 2 \, \alpha_1 \, \beta \, \sum X + \frac { (\sum X)^2 } { n } \, \beta^2 - \, 2 \, \beta \sum (X Y) \, - \, 2 \, \alpha_1 \, \sum Y \, + \, 2 \, \overline{X} \, \sum Y \, \beta \, + \, 2 \, \alpha_1 \, \beta \, \sum X \, - \, 2 \, \frac {(\sum X)^2 } { n } \, \beta^2$

ou

$\beta^2 \, \sum X^2 \, + \, n \, \alpha_1^2 \, - \frac { (\sum X)^2 } { n } \, \beta^2 - \, 2 \, \beta \sum (X Y) \, - \, 2 \, \alpha_1 \, \sum Y \, + \, 2 \, \overline{X} \, \sum Y \, \beta$

Esta expressão se separa na soma de duas expressões quadráticas independentes, que podem ser minimizadas usando matemática elementar:

$n \, \alpha_1^2 \, - \, 2 \, \alpha_1 \, \sum Y$

$\beta^2 \, \sum X^2 \, - \frac { (\sum X)^2 } { n } \, \beta^2 - \, 2 \, \beta \sum (X Y) \, + \, 2 \, \frac { \sum X \sum Y } { n } \, \beta$

Cujos valores minimizadores são:

$\alpha_1 \, = \, \frac { \sum Y } { n }$

$\alpha \, = \, \overline{Y} \, - \, \overline{X} \, \beta$

$\beta \, = \, \frac { n \, \sum (X Y) - \sum X \sum Y } { n \, \sum X^2 - (\sum X)^2 }$

Memorização

Uma forma fácil de memorizar esta expressão é escrever:

$Y = \alpha + X \beta$

$XY = X \alpha + X^2 \beta$

e, em seguida, somar as colunas:

$\sum Y = n \alpha + \sum X \beta$

$\sum (XY) = \sum X \alpha + \sum (X^2) \beta$

Intervalos de confiança

O valor estimato de $\beta\,$ , $\hat{\beta}\,$ , deve ser analisado através da distribuição t de Student, porque

$t = \frac {(\hat{\beta} - \beta) \ \sqrt{n - 2} \ \sqrt{\sum(X_i - \overline{X})^2}} {\sqrt{\sum \hat{\epsilon_i}^2}},$

tem a distribuição t de Student com n-2 graus de liberdade (ver Fisher, R. A. (1925). "Applications of "Student's" distribution". Metron 5: 90–104.), em que:

$\hat{\epsilon_i} = Y_i - \hat{\beta} \ X_i - \hat{\alpha}\,$

A variância de $\epsilon_i\,$ , $\sigma^2\,$ pode ser estimada através dos erros observados:

$\chi_{n-2}^2 = \frac {\sum \hat{\epsilon_i}^2} {\sigma^2}$

se distribui como uma Chi quadrado com n-2 graus de liberdade.

Bibliografia

REIS, E., Estatistica Descritiva (2ª ed.). Lisboa: Edições Sílabo, 1994

Esta página usa conteúdo da Wikipedia. O artigo original estava em Regressão_linear. Tal como o Think Finance neste artigo, o texto da Wikipedia está disponível segundo a GNU Free Documentation License.

Revisão das 11h41min de 13 de outubro de 2008 (ver código-fonte) Incognitus (discussão \| contribs) ← Edição anterior		Edição atual desde as 12h27min de 13 de outubro de 2008 (ver código-fonte) Incognitus (discussão \| contribs)
Linha 1:		Linha 1:
		+	[[Image:LinearRegression.png\|thumb\|200px\|Exemplo de regressão linear.]]
	Em [[Estatística\|estatística]], '''regressão linear''' é um método para se estimar a condicional (valor esperado) de uma variável ''y'', dados os valores de algumas outras variáveis ''x''.		Em [[Estatística\|estatística]], '''regressão linear''' é um método para se estimar a condicional (valor esperado) de uma variável ''y'', dados os valores de algumas outras variáveis ''x''.

Diferenças entre edições de "Regressão linear"

Edição atual desde as 12h27min de 13 de outubro de 2008

Índice